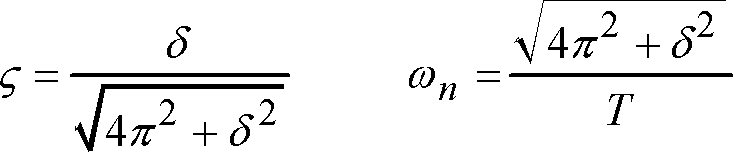What Is Damping Ratio Formula

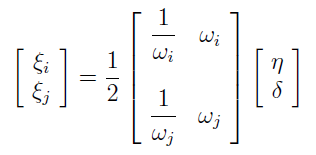
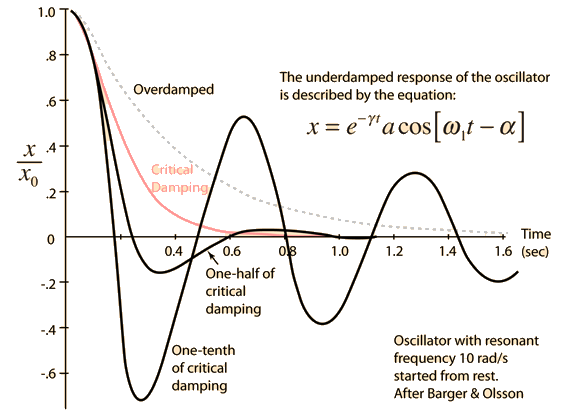
So the system is underdamped and will oscillate back and forth before coming to rest.

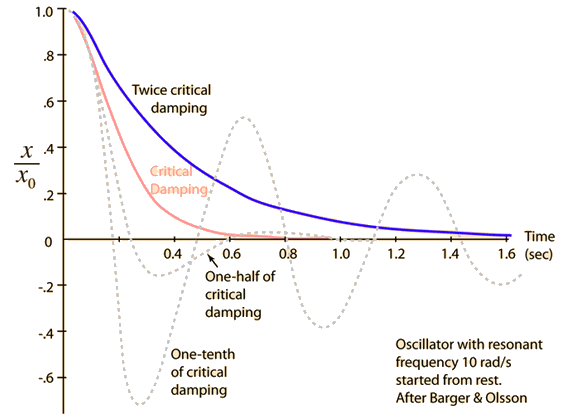
What is damping ratio formula. The behaviour of oscillating systems is often of interest in a diverse range of disciplines that include control engineering chemical engineering mechanical engineering structural engineering and electrical engineering. Displaystyle df frac z mathrm load z mathrm source solving for. Many systems exhibit oscillatory behavior when they are disturbed from their position of static equilibrium. Critical damping coefficient 2 x the square root of k x m 2 x the square root of 100 x 10 63 2 ns m.

The constant ζ is known as the damping ratio or factor and ωn as the undamped natural angular frequency. Since the actual damping coefficient is 1 ns m the damping ratio 1 63 2 which is much less than 1. D f z l o a d z s o u r c e. A mass suspended from a spring for example might if pulled and released bounce up and down.

I still don t get how to calculate the damping ratio for the data supplied by bilstein. So the system is underdamped and will oscillate back and forth before coming to rest. The damping ratio is a system parameter denoted by ζ zeta that can vary from undamped ζ 0 underdamped ζ 1 through critically damped ζ 1 to overdamped ζ 1. For ζs 0 5 and es ef 1 the effective damping ratio decreases from 5 to 3 33 in the anti symmetric vibration mode and from 5 to 2 66 in the symmetric vibration mode.

Since the actual damping coefficient is 1 ns m the damping ratio 1 63 2 which is much less than 1. What is its damping ratio. Z s o u r c e. Formula first contributed by.

Z s o u r c e. Thus with a unit step input. Displaystyle z mathrm source output impedance are shown in the diagram. Trooper in engineering the damping ratio is a dimensionless measure describing how oscillations in a system decay after a disturbance.

These changes indicate that the flexibility of the foundation rock affects the response of the dam in its symmetric vibration modes more than in its anti symmetric modes.